全等三角形指两个全等的三角形,它们的三条边及三个角都对应相等。根据全等转换,两个全等三角形经过平移、旋转、翻折后,仍旧全等。
在学习的过程中,文字与图片相结合能够更好地理解某一内容,针对全等三角形的知识,本篇文章将借助博思在线协作白板这款免费工具为大家绘制全等三角形的思维导图以便理解,同时也让大家彻彻底底搞懂这一块的内容。
1. 全等三角形的性质
全等三角形的对应角和对应边相等;对应边上的高和中线对应相等,对应角的角平分线也相等。全等三角形中,能够完全重合的顶点叫对应顶点。此外,全等三角形的面积和周长相等,对应角的三角函数值相等。

2. 全等三角形的判定
全等三角形有5种判定方式:
-
SSS(边边边):三边对应相等的三角形是全等三角形
-
SAS(边角边):两边及其夹角对应相等的三角形是全等三角形
-
ASA(角边角):两角及其夹边对应相等的三角形全等
-
AAS(角角边):两角及其一角的对边对应相等的三角形全等
-
RHS(直角、斜边、边):又称HL定理(斜边、直角边)在一对直角三角形中,斜边及另一条直角边相等(SSS原理)
要注意的是,下面两种方法不能验证为全等三角形:
-
AAA(角角角):三角相等,不能证全等,但能证相似三角形
-
SSA(边边角):其中一角相等,且非夹角的两边相等
在学习了全等三角形的判定条件后,该如何进行判定呢?从判定条件可知,要判定两个三角形全等,需要知道这两个三角形分别有3个元素(至少一个元素是边)对应相等,这样就可以利用题目中的已知边(角)去迅速准确地确定要补充的边(角),因此,判定两个三角形全等的思路有:
-
已知两边:找夹角(SAS) 或 找另一边(SSS)
-
已知一边一角:若边为角的对边,找任一角(AAS);若边就是角的一条边,则找这条边上的另一角(ASA) 或 找这条边上的对角(AAS) 或 找该角的另一边(SAS)
-
已知两角:找两角的夹边(ASA) 或 找任一边(AAS)
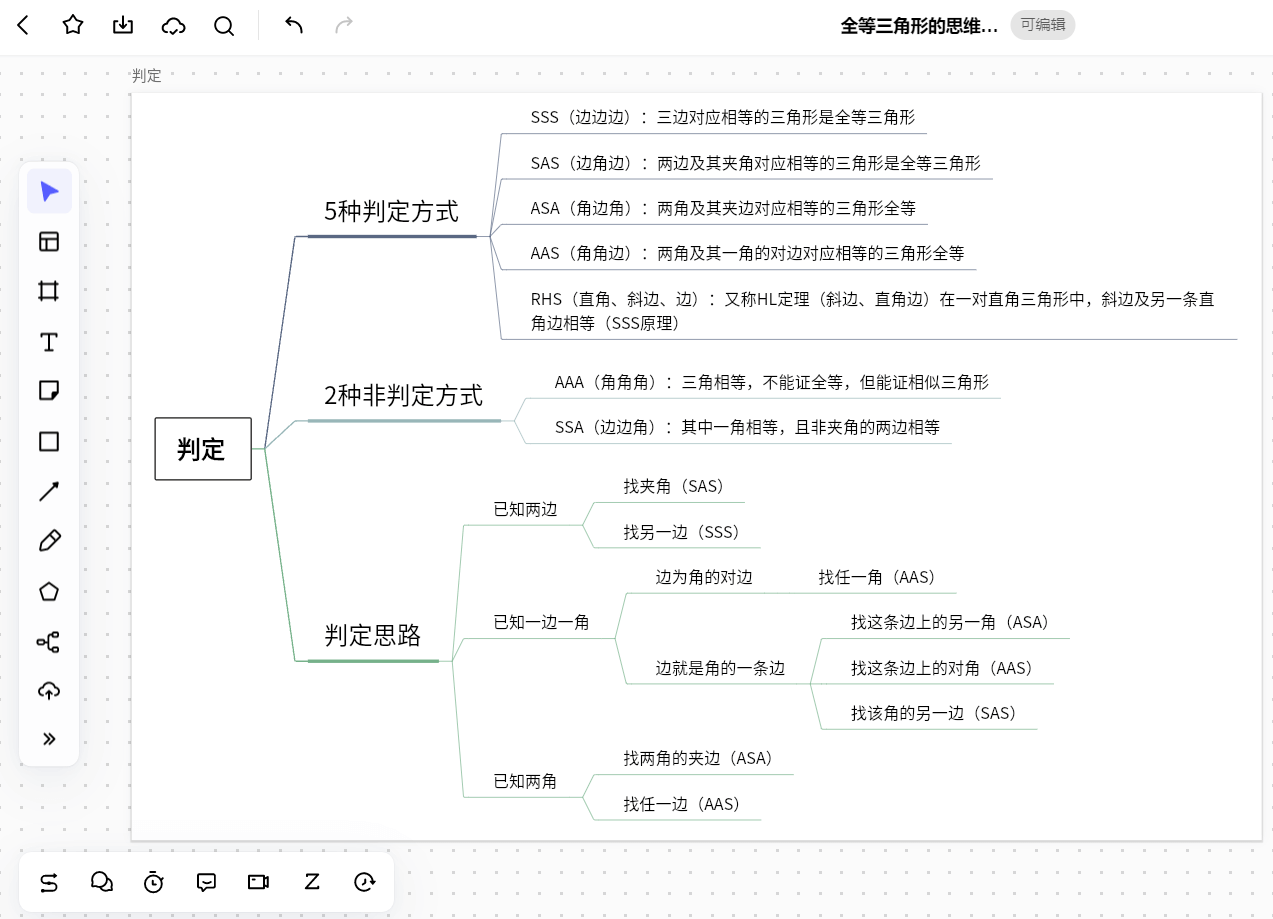
以下就是绘制好的全等三角形的思维导图:
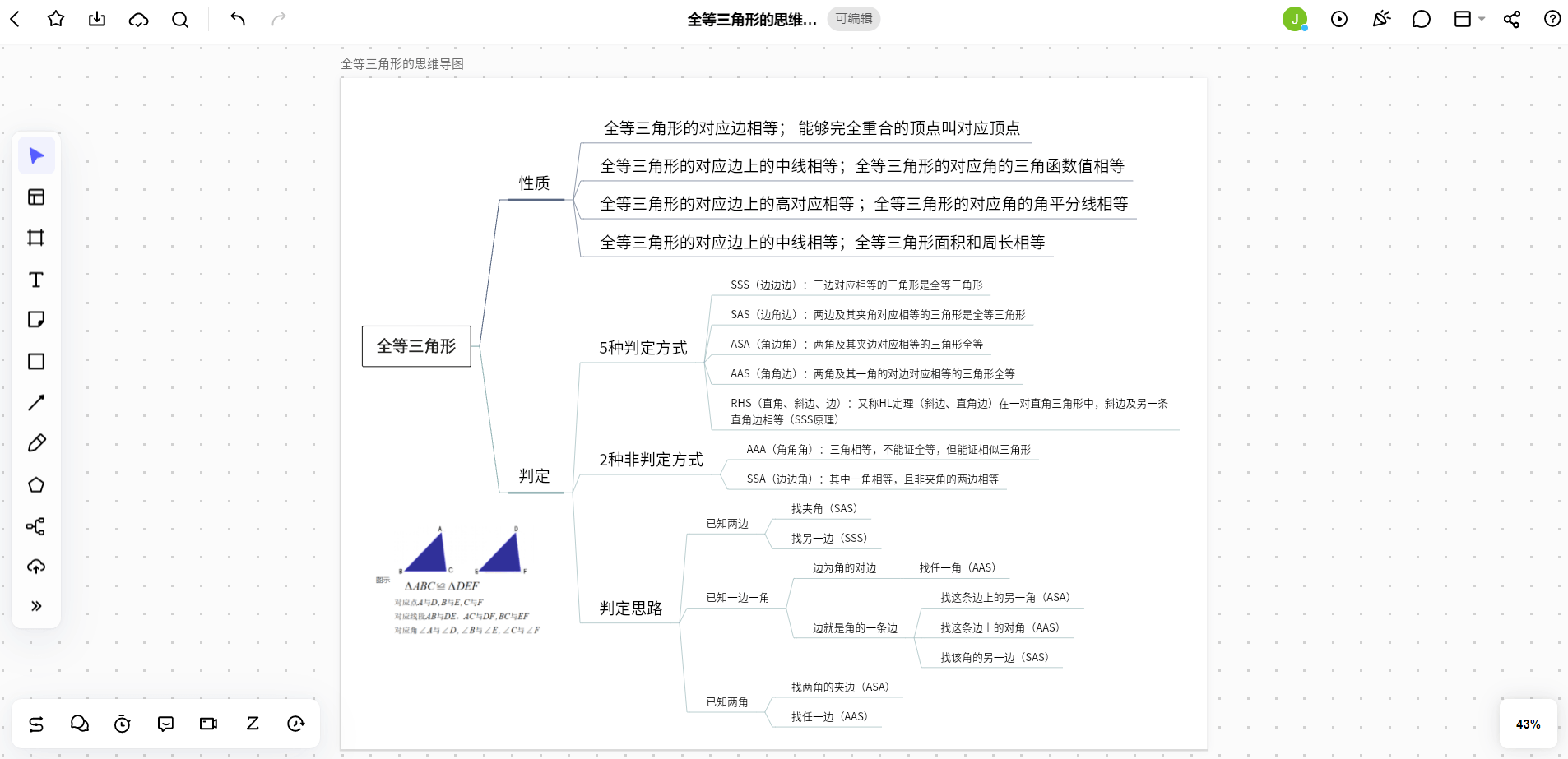
3. 绘制全等三角形思维导图的工具
采用传统手绘的方式绘制全等三角形的思维导图不仅费时,还不好保存,思维也会受限于一张白纸上,而使用博思白板绘制全等三角形的思维导图有着如下优势:
- 无限画布、释放创意
博思在线协作白板拥有无限延伸的画布,并且所有的基本元素都可以自由编辑、无限放大。
- 云端保存、无限扩容
博思在线协作白板是一款轻量级的可视化在线协作白板工具,基于Web网页端运行,对用户本地设备的资源消耗较少。访问网页即可创建白板,不受平台及客户端限制,只要处于联网状态,创建的白板内容都会被自动保存,实时共享。
- 线上协作、实时沟通
支持多人实时在线编辑,可实现直播级同步。还支持接入腾讯会议、飞书会议、钉钉会议、Zoom、瞩目、企业微信等第三方语音/视频会议软件,帮助你和团队成员一起在线协作,肆意挥洒创造力和想象力。
如果你想绘制思维导图或者其他图表,都可以进入博思在线协作白板进行学习,这块白板工具模板丰富,总会有你所需要的模板。