鸡兔同笼问题是小学数学中经典的题目之一,它能锻炼到小学生的数学思维,由于它的解法不止一种,因而又可以开阔学生的视野。尽管鸡兔同笼是一种十分有趣的数学题目,但对于不少学生来说,它比较复杂,学起来也有点吃力。因此,将鸡兔同笼相关问题和解法梳理清楚十分有必要。本篇文章将使用BoardMix博思在线协作白板绘制四年级鸡兔同笼思维导图,一起来看看吧!
1. 鸡兔同笼历史背景
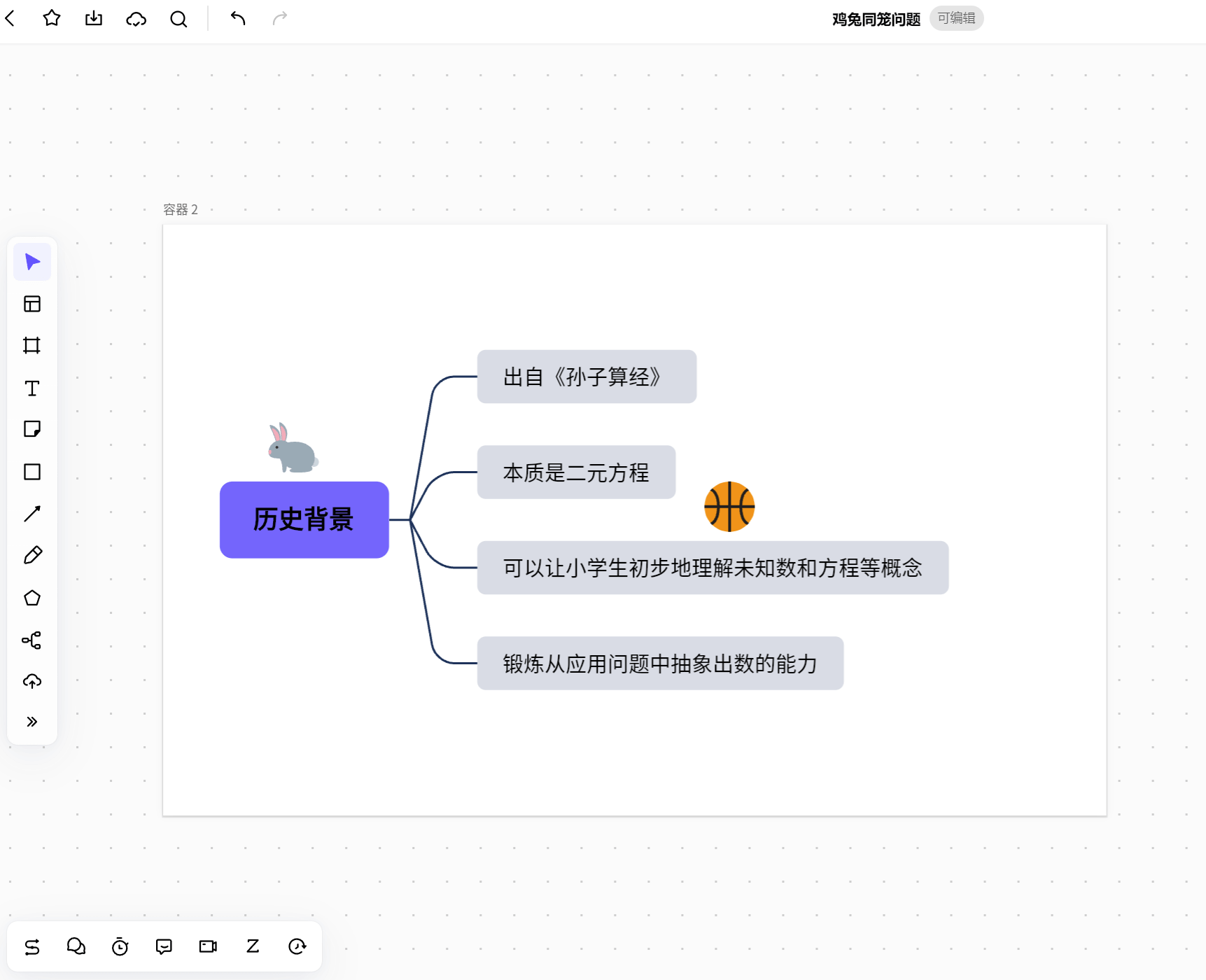
鸡兔同笼是中国古代的数学名题之一。大约在1500年前,《孙子算经》中就记载了这个有趣的问题。书中是这样叙述的:今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?
这一问题的本质是一种二元方程。如果教学方法得当,可以让小学生初步地理解未知数和方程等概念,并锻炼从应用问题中抽象出数的能力。
同一本书中还有一道变题:
今有兽,六首四足;禽,四首二足,上有七十六首,下有四十六足。问:禽、兽各几何?答曰:八兽、七禽。
题设条件包括了不同数量的头和不同数量的足。我们可以使用BoardMix博思在线白板绘制出详细的鸡兔同笼历史背景思维导图。
2. 鸡兔同笼解题思路
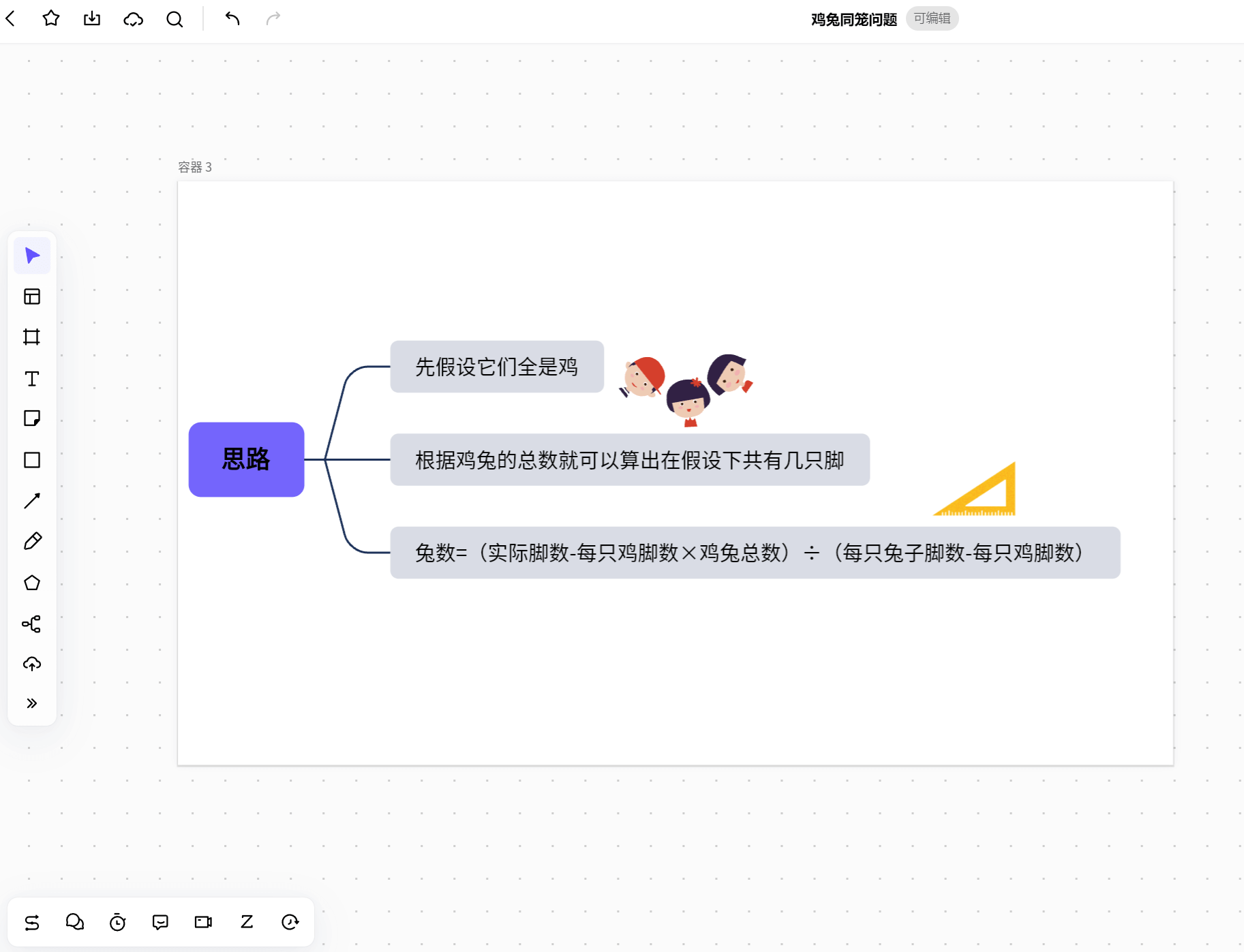
如果先假设它们全是鸡,于是根据鸡兔的总数就可以算出在假设下共有几只脚,把这样得到的脚数与题中给出的脚数相比较,看看差多少,每差2只脚就说明有1只兔,将所差的脚数除以2,就可以算出共有多少只兔。
概括起来,解鸡兔同笼题的基本关系式是:兔数=(实际脚数-每只鸡脚数×鸡兔总数)÷(每只兔子脚数-每只鸡脚数)。类似地,也可以假设全是兔子。
同样,我们可以使用BoardMix博思在线白板来绘制出鸡兔同笼问题的思路思维导图。
3. 鸡兔同笼本质解法
- 假设法
假设法是小学生比较常用的方法。假设全是兔,则(总头数×每只兔的脚数-总脚数)÷(每只兔的脚数-每只鸡的脚数)=鸡的数量;假设全是鸡,则(总脚数-总头数×每只兔的脚数)÷(每只兔的脚数-每只鸡的脚数)=兔子的数量。
利用这个公式我们就很容易列出式子,假设有35只兔子,鸡的数量=(35×4-94)÷(4-2)=23只,兔子的数量=35-23=12只。
为了方便记忆,有人总结出了口诀:假设全是鸡,假设全是兔,多了几只脚,少了几只足?除以脚之差,便是鸡兔数。
- 列方程法
列方程法是初中生比较常用的解题方法,可列一元一次方程,也可列二元一次方程组。鸡兔同笼问题里含有两个等量关系:
(1)鸡脚的总数+兔脚的总数=总脚数;(2)鸡的总头数+兔的总头数=总头数。
若列一元一次方程,可设鸡的总头数为x头,那么兔的总头数为(35-x)头,根据脚数的等量关系可以列出方程2x+4(35-x)=94,解方程即可得出答案。
若列二元一次方程组,可设兔有x只,鸡有y只,得到x+y=35和4x+2y=94两个方程,联合解方程组即可。
- 古典法
对于鸡兔同笼问题的解决办法,《孙子算经》的作者给出了两个公式,最简单的一个公式:上置头,下置足,半其足,以头除足,以足除头,即得。也就是兔子的只数=总腿数÷2-总只数。根据这个公式我们很容易得到,兔子的数量=94÷2-35=12只。这种解法在今天也被称为“抬腿法”。
- 《孙子算法》解法
在算筹盘第一行摆上数字三十五,第二行摆上数字九十四,将脚数除以二,此时第一行是三十五,第二行是四十七。用较小的头数减去较多的半脚数,四十减去三十(上三除下四),七减去五(上五除下七)。此时下行是十二,三十五减十二(下一除上三,下二除上五)得二十三。此时第一行剩下的算筹就是鸡的数目,第二行的算筹就是兔的数目。

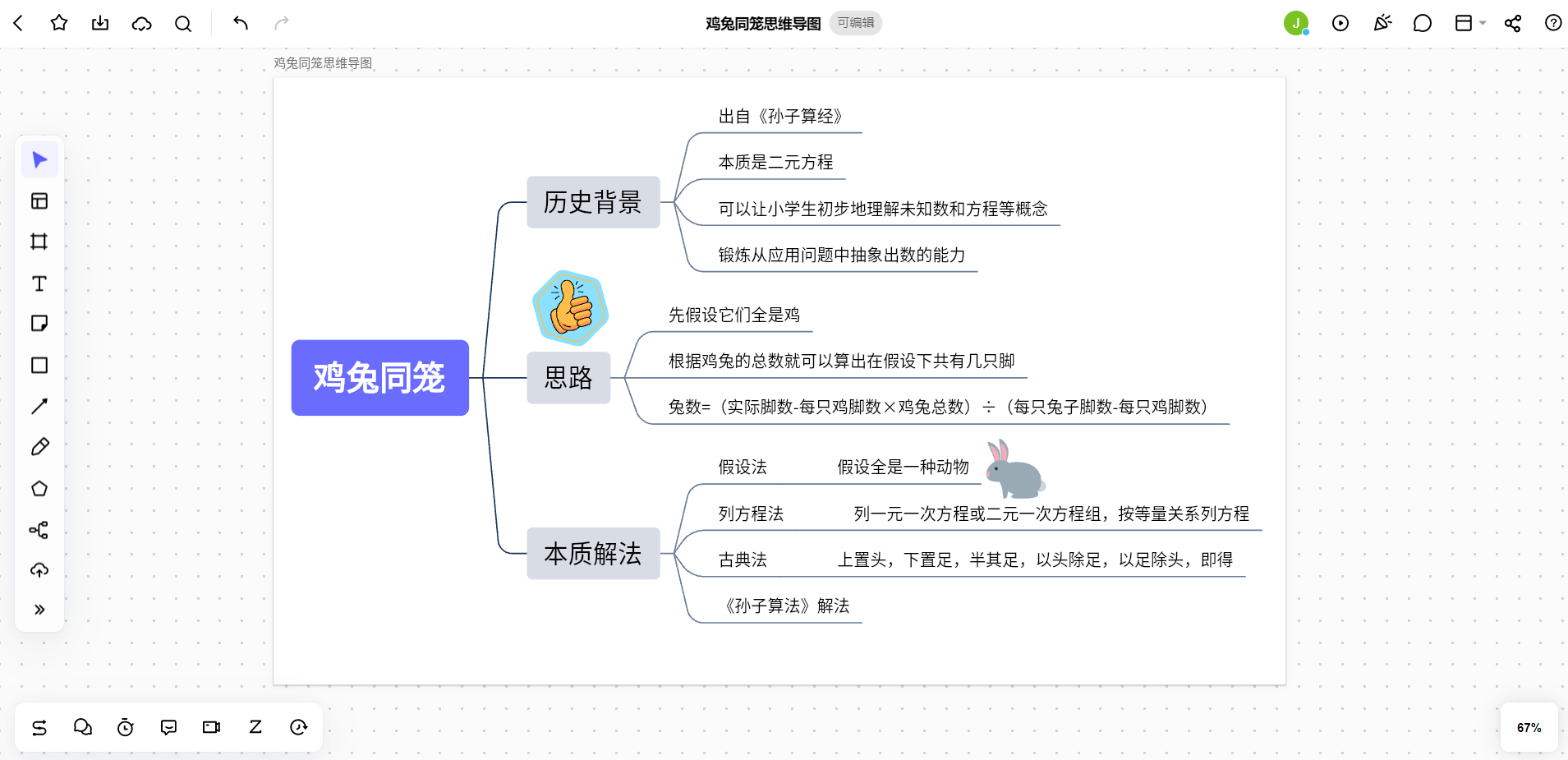
至此,四年级鸡兔同笼思维导图便完成了,将其汇总到一张图上,不仅可以形成自己的知识体系,还能在以后的复习中使用。
BoardMix博思白板是一款综合性的在线白板软件,它可以用来绘制思维导图、流程图、概念图、鱼骨图、组织结构图、时间线等多种图表;支持团队协作,可多人实时在线编辑同一份思维导图文件;提供个人免费版,满足基本绘图需求!免费又好用!